Permutation

Practice Problems

1. How many different ways can you arrange the letters of the alphabet?

Solution

There are 26 letters in the alphabet. 26 objects can be arranged in 26! different ways (that's more than 400 000 000 000 000 000 000 000 000 different arrangements!!!)


2. How many different ways can you arrange the letters of the word "VISITING"? How many of these arrangements have all three I's next to each other?

Solution

VISITING has 8 letters, thus there are 8! ways to arrange these letters. However, there are three I's which cannot be distingished from each other. These three I's can be interchanged 3! different ways. Thus there are a total of 8! / 3! distinct arrangements of VISITING.

To determine how many of the arrangements of VISITING have all three I's next to each other, we may complete a similar problem: How many different ways can VSTNG[III] be arranged? Note that the three I's are treated as one character. Thus 6 different symbols can be arranged 6! times - and these arrangements are all the arrangements of VISITING where the I's are next to each other.



3. Determine how many different five-digit numbers may be made from the digits 4, 3, 7, 8, and 9. How many of these numbers are even? How many are odd? How many start with the number 7?

Solution

There are 5! different ways to arrange the five digits 4, 3, 7, 8, and 9.

The even numbers are those which end in either 4 or 8. Since either 4 or 8 must be chosen for the last digit, there are only two choices for the last digit. In addition, there are four numbers left to pick from for the first digit, three for the second digit, two for the third digit, and one left for the fourth digit. This corresponds to...

2 * 4 * 3 * 2 * 1 = 48 even numbers.


Similar to the previous problem, there are 3 choices for the "last digit" (3, 7, 9) to make the number odd. After that, there are 4 numbers left to choose for the first digit, 3 numbers for the second, and so on. Thus, there are...

3 * 4 * 3 * 2 * 1 = 72 odd numbers.


Another way to solve this problem is to realize that out of the 5! = 120 ways to arrange the five digits, these arrangements must be either even or odd. Since there are 48 even numbers, there must be 120 - 48 = 72 odd numbers.

If the number must start with 7, there is only one choice for the first digit. There are four for the second digit, 3 for the third, and so on. In all, there are

1 * 4 * 3 * 2 * 1 = 24 numbers beginning with 7.




4. Josˇ has seven cookbooks on a shelf. Four of them deal with Italian food, and three of them are concerned with Greek food. How many ways can he arrange the cookbooks...





Solution

With no restrictions, there are 7! ways to arrange seven cookbooks.

If the food styles must alternate, they will be arranged GTGTGTG (G = Greek, T = Italian). There are 4 choices of Greek books for the first slot, 3 choices of Italian books for the second slot, 3 Greek book left for the third spot, 2 Italian books for the next slot, and so on. Thus, the cookbooks may be arranged 4 * 3 * 3 * 2 * 2 * 1 * 1 = 144 different ways.

Since the Greek cookbooks must be adjacent, consider them as one unit and determine the number of ways to permute...

[GGGG]TTT


There are 4! ways to permute these four objects. However, note that the Greek cookbooks themselves may be arranged 4! ways - thus there are 4! * 4! = 576 ways to arrange the Greek cookbooks next to each other.

If all the Greek cookbooks must be next to each other, and all the Italian cookbooks must be next to each other there are two possible scenarios:

GGGGTTT or TTTGGGG


GGGGTTT may be arranged 4! * 3! ways. The Greek books may be interchanged 4! ways; for each of these arrangements, the Italian books may be arranged 3! different ways. Thus there are 4! * 3! arrangements for GGGGTTT. If the cookbooks are aligned TTTGGGG, it is the same. Thus there are 4! * 3! + 4! * 3! = 2 * 4! * 3! = 288 ways to arrange the cookbooks in this fashion.



5. Marion is standing on the corner of Madison Street and Commonwealth Avenue. How many different routes may she take when driving to the supermarket?


Solution

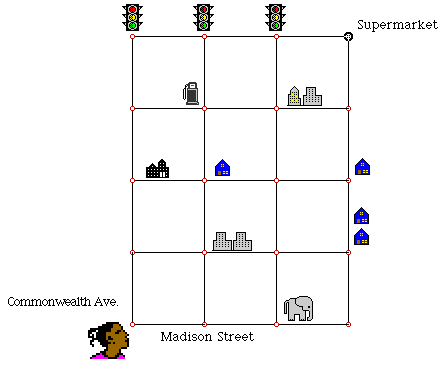
For Marion to arrive at the supermarket, she must travel east 3 blocks and north 4 blocks. One way for her to get there would be to travel east, east, north, north, north, north, east. Another way is north, east, north, east, north, north, east. No matter what though, she must travel 3 blocks east, and 4 blocks north. Therefore, we may find the total possible travel routes by finding the number of permutations of:

EEENNNN


These digits may be arranged
7! = 35
3! * 4!
different ways; therefore there are 35 ways for Marion to travel to the supermarket.





[Cardmeister Home] [Permutation] [Combinations] [Probability] [Links] [Feedback]